Bayesian Statistics Lab#
In this hands-on lab, we continue our demonstration of “estimating the mass of a new fundamental particle”. We will generate multiple experiments, each giving a noisy measurement of the particle’s mass, and sequentially update our posterior distribution after each experiment. We will then discuss what we should do when new theoretical prior appears.
Physical Setup (Brief Recap)#
Let’s update some notation from the notes.
We have a particle of true mass \(m_\text{true}\), measured in TeV. Each experiment yields an observed mass \(m_\text{obs}\) with Gaussian noise:
(293)#\[\begin{align}
m_\text{obs} \;\sim\; \mathcal{N}(m_\text{true},\sigma_\text{expr}^2).
\end{align}\]
Here, \(\sigma_\text{expr}\) is the detector resolution or statistical uncertainty.
We know that \(m_\text{true}\) lies in some range \([2,8]\) TeV—our initial theory suggests it cannot be outside this window. Hence, our initial prior:
(294)#\[\begin{align}
p(\theta) =
\begin{cases}
1/(8 - 2), & 2 \le \theta \le 8, \\
0, & \text{otherwise}.
\end{cases}
\end{align}\]
Each measurement modifies our belief (the prior) into a posterior via Bayes’ Theorem:
(295)#\[\begin{align}
p(m \mid m_{\text{obs}}) \propto p(m_{\text{obs}} \mid m) \, p(m).
\end{align}\]
Here, the likelihood \(p(m_\text{obs} \mid m_\text{true})\) is given by the Gaussian formula:
(296)#\[\begin{align}
p(m_{\text{obs}} \mid m) = \frac{1}{\sqrt{2\pi}\,\sigma_\text{expr}} \exp\left[-\frac{(m_{\text{obs}}-m)^2}{2\sigma_\text{expr}^2}\right].
\end{align}\]
Single Experiment Code (Grid Approximation)#
Please rewrite the code in the class note into multiple functions that we can perform numerical experiments.
import numpy as np
import matplotlib.pyplot as plt
# For reproducibility
np.random.seed(42)
# HANDSON: Define range for m (0 to 10 TeV)
ms = np.linspace(0, 10, 1001)
# HANDSON: Gaussian likelihood
def likelihood(x, x0, sigma):
norm = 1.0 / (np.sqrt(2*np.pi) * sigma)
return norm * np.exp(-0.5 * ((x-x0) / sigma)**2)
def run_expr(
prior, # Prior before updated by the experiment
m_true, # Suppose this is the true mass
sigma_expr, # Detector resolution
seed = None, # For reproducibility
):
if seed is not None:
np.random.seed(seed)
# HANDSON: By running an experiment, we obtain a single measurement
# You may use np.random.normal().
m_obs = np.random.normal(loc=m_true, scale=sigma_expr)
# HANDSON: Posterior ~ prior * likelihood
like = likelihood(m_obs, ms, sigma_expr)
unnorm_post = like * prior
# HANDSON: Normalize the posterior
norm = 1 / np.trapezoid(unnorm_post, ms)
post = norm * unnorm_post
return m_obs, post
# Uniform prior in [2, 8]
def prior0(ms, m_min=2, m_max=8):
# HANDSON: Uniform in [2,8], zero outside
return np.where((m_min <= ms) & (ms <= m_max), 1/(m_max-m_min), 0)
# Compute prior
prior = prior0(ms)
# Run a numerical experiment
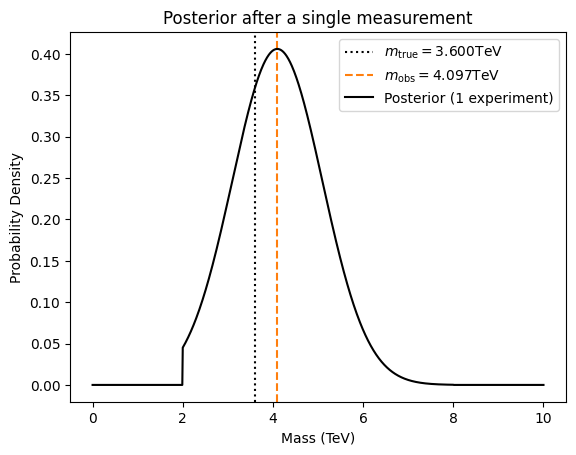
m_true = 3.6 # Set the groundtruth
sigma_expr = 1.0 # Detector resolution
m_obs, post = run_expr(prior, m_true, sigma_expr)
plt.axvline(m_true, ls=':', color='k', label=r"$m_\text{true}="+f"{m_true:.3f}$TeV")
plt.axvline(m_obs, ls='--', color='C1', label=r"$m_\text{obs}= "+f"{m_obs:.3f}$TeV")
plt.plot(ms, post, 'k', label="Posterior (1 experiment)")
plt.title("Posterior after a single measurement")
plt.xlabel("Mass (TeV)")
plt.ylabel("Probability Density")
plt.legend()
<matplotlib.legend.Legend at 0x7ff3db56a300>
Multiple Experiments#
Now we simulate \(N\) experiments. Each experiment provides \((m_{\text{obs},i}, \sigma_i) = (m_{\text{obs},i}, \sigma_\text{expr})\). We update our posterior step by step:
Start with the prior (initially uniform in \([2,8]\)).
For each experiment \(i\), multiply the current posterior by the new likelihood.
Normalize to get the updated posterior, which becomes the prior for the next experiment.
# For reproducibility
np.random.seed(42)
# HANDSON: Let's simulate multiple experiments
m_true = 1.5 # Set the groundtruth
sigma_expr = 1.0 # Detector resolution
N = 100 # Number of experiments
ms_obs = np.random.normal(m_true, sigma_expr, N) # Draw N samples from a normal distribution. You may use np.random.normal().
print("Simulated experiment results:")
for i, m_obs in enumerate(ms_obs):
print(f"\tExperiment {i+1}: observed mass = {m_obs:.3f} ± {sigma_expr:.3f}")
Simulated experiment results:
Experiment 1: observed mass = 1.997 ± 1.000
Experiment 2: observed mass = 1.362 ± 1.000
Experiment 3: observed mass = 2.148 ± 1.000
Experiment 4: observed mass = 3.023 ± 1.000
Experiment 5: observed mass = 1.266 ± 1.000
Experiment 6: observed mass = 1.266 ± 1.000
Experiment 7: observed mass = 3.079 ± 1.000
Experiment 8: observed mass = 2.267 ± 1.000
Experiment 9: observed mass = 1.031 ± 1.000
Experiment 10: observed mass = 2.043 ± 1.000
Experiment 11: observed mass = 1.037 ± 1.000
Experiment 12: observed mass = 1.034 ± 1.000
Experiment 13: observed mass = 1.742 ± 1.000
Experiment 14: observed mass = -0.413 ± 1.000
Experiment 15: observed mass = -0.225 ± 1.000
Experiment 16: observed mass = 0.938 ± 1.000
Experiment 17: observed mass = 0.487 ± 1.000
Experiment 18: observed mass = 1.814 ± 1.000
Experiment 19: observed mass = 0.592 ± 1.000
Experiment 20: observed mass = 0.088 ± 1.000
Experiment 21: observed mass = 2.966 ± 1.000
Experiment 22: observed mass = 1.274 ± 1.000
Experiment 23: observed mass = 1.568 ± 1.000
Experiment 24: observed mass = 0.075 ± 1.000
Experiment 25: observed mass = 0.956 ± 1.000
Experiment 26: observed mass = 1.611 ± 1.000
Experiment 27: observed mass = 0.349 ± 1.000
Experiment 28: observed mass = 1.876 ± 1.000
Experiment 29: observed mass = 0.899 ± 1.000
Experiment 30: observed mass = 1.208 ± 1.000
Experiment 31: observed mass = 0.898 ± 1.000
Experiment 32: observed mass = 3.352 ± 1.000
Experiment 33: observed mass = 1.487 ± 1.000
Experiment 34: observed mass = 0.442 ± 1.000
Experiment 35: observed mass = 2.323 ± 1.000
Experiment 36: observed mass = 0.279 ± 1.000
Experiment 37: observed mass = 1.709 ± 1.000
Experiment 38: observed mass = -0.460 ± 1.000
Experiment 39: observed mass = 0.172 ± 1.000
Experiment 40: observed mass = 1.697 ± 1.000
Experiment 41: observed mass = 2.238 ± 1.000
Experiment 42: observed mass = 1.671 ± 1.000
Experiment 43: observed mass = 1.384 ± 1.000
Experiment 44: observed mass = 1.199 ± 1.000
Experiment 45: observed mass = 0.021 ± 1.000
Experiment 46: observed mass = 0.780 ± 1.000
Experiment 47: observed mass = 1.039 ± 1.000
Experiment 48: observed mass = 2.557 ± 1.000
Experiment 49: observed mass = 1.844 ± 1.000
Experiment 50: observed mass = -0.263 ± 1.000
Experiment 51: observed mass = 1.824 ± 1.000
Experiment 52: observed mass = 1.115 ± 1.000
Experiment 53: observed mass = 0.823 ± 1.000
Experiment 54: observed mass = 2.112 ± 1.000
Experiment 55: observed mass = 2.531 ± 1.000
Experiment 56: observed mass = 2.431 ± 1.000
Experiment 57: observed mass = 0.661 ± 1.000
Experiment 58: observed mass = 1.191 ± 1.000
Experiment 59: observed mass = 1.831 ± 1.000
Experiment 60: observed mass = 2.476 ± 1.000
Experiment 61: observed mass = 1.021 ± 1.000
Experiment 62: observed mass = 1.314 ± 1.000
Experiment 63: observed mass = 0.394 ± 1.000
Experiment 64: observed mass = 0.304 ± 1.000
Experiment 65: observed mass = 2.313 ± 1.000
Experiment 66: observed mass = 2.856 ± 1.000
Experiment 67: observed mass = 1.428 ± 1.000
Experiment 68: observed mass = 2.504 ± 1.000
Experiment 69: observed mass = 1.862 ± 1.000
Experiment 70: observed mass = 0.855 ± 1.000
Experiment 71: observed mass = 1.861 ± 1.000
Experiment 72: observed mass = 3.038 ± 1.000
Experiment 73: observed mass = 1.464 ± 1.000
Experiment 74: observed mass = 3.065 ± 1.000
Experiment 75: observed mass = -1.120 ± 1.000
Experiment 76: observed mass = 2.322 ± 1.000
Experiment 77: observed mass = 1.587 ± 1.000
Experiment 78: observed mass = 1.201 ± 1.000
Experiment 79: observed mass = 1.592 ± 1.000
Experiment 80: observed mass = -0.488 ± 1.000
Experiment 81: observed mass = 1.280 ± 1.000
Experiment 82: observed mass = 1.857 ± 1.000
Experiment 83: observed mass = 2.978 ± 1.000
Experiment 84: observed mass = 0.982 ± 1.000
Experiment 85: observed mass = 0.692 ± 1.000
Experiment 86: observed mass = 0.998 ± 1.000
Experiment 87: observed mass = 2.415 ± 1.000
Experiment 88: observed mass = 1.829 ± 1.000
Experiment 89: observed mass = 0.970 ± 1.000
Experiment 90: observed mass = 2.013 ± 1.000
Experiment 91: observed mass = 1.597 ± 1.000
Experiment 92: observed mass = 2.469 ± 1.000
Experiment 93: observed mass = 0.798 ± 1.000
Experiment 94: observed mass = 1.172 ± 1.000
Experiment 95: observed mass = 1.108 ± 1.000
Experiment 96: observed mass = 0.036 ± 1.000
Experiment 97: observed mass = 1.796 ± 1.000
Experiment 98: observed mass = 1.761 ± 1.000
Experiment 99: observed mass = 1.505 ± 1.000
Experiment 100: observed mass = 1.265 ± 1.000
# HANDSON: compute the prior from prior0()
prior = prior0(ms)
# Perform sequential Bayesian updates using the same grid approach
plt.figure(figsize=(8,5))
plt.axvline(m_true, color='k', ls=':', label=r'$m_\text{true}$')
plt.plot(ms, prior, label="Initial Prior", lw=2)
for i, m_obs in enumerate(ms_obs):
# HANDSON: compute the posterior
m_obs, post = run_expr(prior, m_true, sigma_expr)
# Plot the posterior
if i % 20 == 19:
plt.plot(ms, post, label=f"Posterior after Exp {i+1}")
# HANDSON: posterior becomes prior for next iteration
prior = post
plt.title("Sequential Bayesian Updates of Particle Mass")
plt.xlabel("Mass (TeV)")
plt.ylabel("Probability Density")
plt.legend()
<matplotlib.legend.Legend at 0x7ff3db5d9f70>
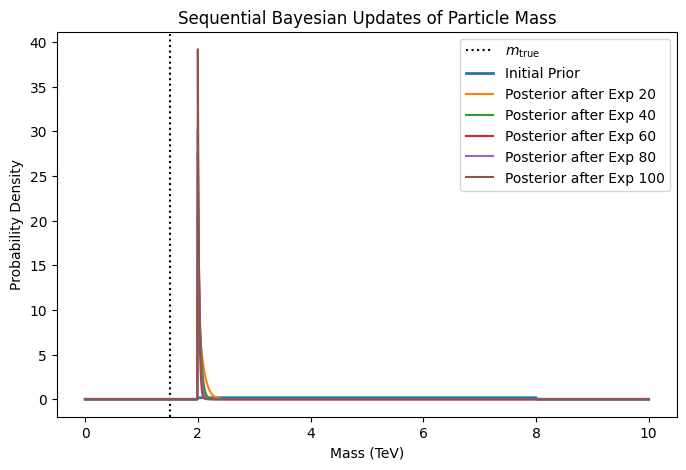
You will see each new experiment narrowing or shifting the distribution.
# HANDSON:
# Try to increase `N` to, e.g, 100 and plot the posterior every 10 experiments.
# What do you see?
# HANDSON:
# Try to change `m_true` to a value outside the theory, e.g., 1.5, and plot the posterior.
# What do you see?
# HANDSON:
# Suppose now there are two theories, one suggests the mass range [2,8] TeV,
# one suggests the mass range [1,5] TeV.
# How would you take this new theory into account?
# Try implement your idea(s) and interpret the results.