Derivatives Lab Solution

This lab allows students to experiment with different differentiation methods, including symbolic, finite difference, complex step differentiation, and automatic differentiation.

Symbolic Differentiation with SymPy

We first try out symbolic differentiation using scipy. This is very similar to the class notes, except we will take derivatives of the \(\text{sinc}(x) = \sin(x) / x\).

# HANDSON: make sure that sympy is installed

!pip install sympy

import sympy as sp

Requirement already satisfied: sympy in /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages (1.13.3)
Requirement already satisfied: mpmath<1.4,>=1.1.0 in /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages (from sympy) (1.3.0)

# HANDSON: use sympy to define the equation f(x) = sin(x) / x ...

x = sp.symbols('x')
f = sp.sin(x) / x

# HANDSON: ... and get its derivative

f_prime = sp.diff(f, x)
f_prime_simplified = sp.simplify(f_prime)

# Display f'(x)

f_prime

\[\displaystyle \frac{\cos{\left(x \right)}}{x} - \frac{\sin{\left(x \right)}}{x^{2}}\]

# Display simplified f'(x)

f_prime_simplified

\[\displaystyle \frac{x \cos{\left(x \right)} - \sin{\left(x \right)}}{x^{2}}\]

# We didn't do this in the notes,
# but it is possible to obtain numerical values of functions from sympy.

display(f.evalf(subs={x:1}))
display(f_prime_simplified.evalf(subs={x:1}))

\[\displaystyle 0.841470984807897\]

\[\displaystyle -0.301168678939757\]

# HANDSON: modify function `f(x)` and confirm that `sympy` is able to
# compute its derivatives

pass

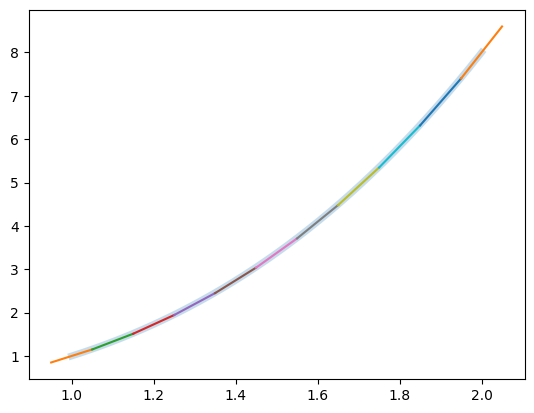
To help visualize the results of derivative, let’s copy the plotting function from the class notes here:

import numpy as np
from matplotlib import pyplot as plt
from typing import Callable

def mkplot(g, X, Fp):
    if isinstance(g, Callable):
        f = g
    else:
        f = lambda x: g.evalf(subs={'x': x})
        
    Xd = np.linspace(min(X), max(X), num=1001)
    Fd = [f(x) for x in Xd]
    
    plt.plot(Xd, Fd, lw=5, alpha=0.25)
    for (x, fp) in zip(X, Fp):
        y = f(x)
        plt.plot(
            [x-0.05,    x+0.05],
            [y-0.05*fp, y+0.05*fp],
        )

X       = range(10)
F_prime = [f_prime.evalf(subs={'x':x}) for x in X]

mkplot(f, X, F_prime)

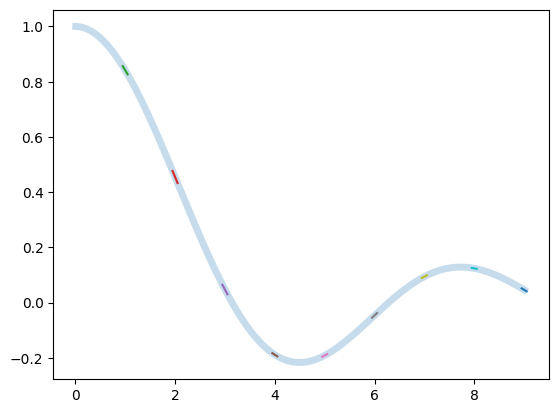
Enhancing Dual Number Autodiff

In the class, we implemented a Dual-number based autodiff scheme. It supports many basic operators except division and power.

Try implementing these extra operators and test them out with our visualization tool.

def V(x):
    """Select the value from a dual number.

    Work for both python built-in numbers (often used in function) and dual numbers.
    """
    if isinstance(x, Dual):
        return x[0]
    else:
        return x

def D(x):
    """Select the derivative from a dual number.

    Work for both python built-in numbers (often used in function) and dual numbers.
    """
    if isinstance(x, Dual):
        return x[1]
    else:
        return 0

class Dual(tuple):
    """Dual number for implementing autodiff in pure python"""

    def __new__(self, v, d=1): # tuple is immutable so we cannot use __init__()
        return tuple.__new__(Dual, (v, d))

    def __add__(self, r):
        return Dual(
            V(self) + V(r),
            D(self) + D(r),
        )
    def __radd__(self, l):
        return self + l # addition commutes

    def __sub__(self, r):
        return Dual(
            V(self) - V(r),
            D(self) - D(r),
        )
    def __rsub__(self, l):
        return Dual(
            V(l) - V(self),
            D(l) - D(self),
        )

    def __mul__(self, r):
        return Dual(
            V(self) * V(r),
            D(self) * V(r) + V(self) * D(r),
        )
    def __rmul__(self, l):
        return self * l # multiplication commutes

    def __truediv__(self, r):
        return Dual(
            V(self) / V(r),
            (D(self) * V(r) - V(self) * D(r)) / (V(r) * V(r)), # HANDSON: implement chain-rule for division
        )
    def __rtruediv__(self, l):
        return Dual(
            V(l) / V(self),
            (D(l) * V(self) - V(l) * D(self)) / (V(self) * V(self)), # HANDSON: implement chain-rule for division
        )

    def __pow__(self, r): # assume r is constant
        if r == 0:
            n = len(V(self))
            return Dual(np.ones(n), np.zeros(n)) # HANDSON: implement chain-rule for power
        elif r == 1:
            n = len(V(self))
            return Dual(V(self), np.ones(n)) # HANDSON: implement chain-rule for power
        else:
            return Dual(
                V(self)**r,
                r*(V(self)**(r-1)) * D(self), # HANDSON: implement chain-rule for power
            )

def sin(x):
    return Dual(
        np.sin(V(x)),
        np.cos(V(x)) * D(x)  # chain rule: d/dx sin(x) = cos(x) * x'
    )

def f(x):
    return x**3
    # return sin(x) / x

X     = np.linspace(1,2,num=11)
F, Fp = f(Dual(X))

mkplot(f, X, Fp)