Numerical Linear Algebra Lab (Solution)

Numerical Linear Algebra Lab (Solution)#

Iterative Solvers: Update Jacobi to Gauss-Seidel#

We learned in the lecture about the Jacobi interation method for solving \(\mathbf{x}\) in the linear equation \(A \mathbf{x} = \mathbf{b}\). The algorithm states that by applying the update rule:

(54)#\[\begin{align} x_i^{(k+1)} = \frac{1}{a_{ii}} \Big(b_i - \sum_{j \neq i} a_{ij} x_j^{(k)}\Big), \end{align}\]

\(x_i^{(k+1)}\) will converge to the solution \(\mathbf{x}\).

We implemeneted and test it in python:

def jacobi_iteration(A, b, max_iter=1000, tol=1e-8):
    """
    Solve A x = b using Jacobi iteration.
    A is assumed to be square with non-zero diagonal.
    """
    n = A.shape[0]
    x = np.zeros(n)
    
    for k in range(max_iter):
        x_old = np.copy(x)
        for i in range(n):
            # Sum over off-diagonal terms
            s = 0.0
            for j in range(n):
                if j != i:
                    s += A[i,j] * x_old[j]
            x[i] = (b[i] - s) / A[i, i]
        
        # Check for convergence
        if np.linalg.norm(x - x_old, ord=np.inf) < tol:
            print(f"Jacobi converged in {k+1} iterations.")
            return x
    
    print("Jacobi did not fully converge within max_iter.")
    return x

import numpy as np

A = np.array([[4.0, -1.0, 0.0],
              [-1.0, 4.0, -1.0],
              [0.0, -1.0, 4.0]], dtype=float)
b = np.array([6.0, 6.0, 6.0], dtype=float)

x_jacobi = jacobi_iteration(A, b)

print("Jacobi solution:", x_jacobi)
print("Direct solve comparison:", np.linalg.solve(A, b))

Jacobi converged in 20 iterations.
Jacobi solution: [2.14285714 2.57142857 2.14285714]
Direct solve comparison: [2.14285714 2.57142857 2.14285714]

For the first hands-on, please update the above Jacobi algorithm and turn it into a working Gauss Seidel algorithm.

Recalling from the lecture that the update step in the Gauss Seidel algorithm is:

(55)#\[\begin{align} x_i^{(k+1)} = \frac{1}{a_{ii}} \Big( b_i - \sum_{j < i} a_{ij} x_j^{(k+1)} - \sum_{j > i} a_{ij} x_j^{(k)} \Big). \end{align}\]

Note that \(\mathbf{x}^{(k+1)}\) is already partially updated (for \(j < i\)).

def gauss_seidel_iteration(A, b, max_iter=1000, tol=1e-8):
    """
    Solve A x = b using the Gauss-Seidel iteration.
    A is assumed to be square with non-zero diagonal.
    """
    n = A.shape[0]
    x = np.zeros(n)

    for k in range(max_iter):
        x_old = np.copy(x)
        for i in range(n):
            # Sum over known terms
            s1 = 0.0
            for j in range(i):
                s1 += A[i, j] * x[j]  # x[j] is updated
            s2 = 0.0
            for j in range(i+1, n):
                s2 += A[i, j] * x_old[j]  # x_old[j] is from previous iteration
            x[i] = (b[i] - s1 - s2) / A[i, i]

        # Check convergence
        if np.linalg.norm(x - x_old, ord=np.inf) < tol:
            print(f"Gauss-Seidel converged in {k+1} iterations.")
            return x

    print("Gauss-Seidel did not fully converge within max_iter.")
    return x

x_gs = gauss_seidel_iteration(A, b)

print("Jacobi solution:", x_jacobi)
print("Gauss-Seidel solution:", x_gs)
print("Direct solve comparison:", np.linalg.solve(A, b))

Gauss-Seidel converged in 11 iterations.
Jacobi solution: [2.14285714 2.57142857 2.14285714]
Gauss-Seidel solution: [2.14285714 2.57142857 2.14285714]
Direct solve comparison: [2.14285714 2.57142857 2.14285714]

Coupled Harmonic Oscillators#

Harmonic oscillators are a classic problem in physics, often forming the basis of more complex vibrational analyses. In this part, you will:

Derive or reference the analytical solution for two coupled oscillators.
Numerically solve the same system (using an eigenvalue approach).
Generalize to \(n\) (and even \(n \times n\)) coupled oscillators, visualizing the mode shapes.

Two Coupled Oscillators–Analytical Solution#

Consider two masses \(m\) connected by three springs (constant \(k\)), arranged in a line and connected to two walls:

|--k--[m]--k--[m]--k--|

If each mass can move only horizontally, the equations of motion form a \(2 \times 2\) eigenvalue problem.

Let:

\(x_1(t)\) be the horizontal displacement of Mass 1 from its equilibrium position.
\(x_2(t)\) be the horizontal displacement of Mass 2.

We assume small oscillations, so Hooke’s law applies linearly.

Mass 1 experiences:
1. A restoring force \(-k \,x_1\) from the left wall spring.
2. A coupling force from the middle spring: if \(x_2 > x_1\), that spring pulls Mass 1 to the right; if \(x_1 > x_2\), it pulls Mass 1 to the left. The net contribution is \(-k (x_1 - x_2)\).
Summing forces (Newton’s second law) gives:

(56)#\[\begin{align} m \, \ddot{x}_1 = -k\,x_1 - k\,(x_1 - x_2). \end{align}\]
Mass 2 experiences:
1. A restoring force \(-k\,x_2\) from the right wall spring.
2. The coupling force from the middle spring: \(-k(x_2 - x_1)\).
Hence,

(57)#\[\begin{align} m \, \ddot{x}_2 = -k\,x_2 - k\,(x_2 - x_1). \end{align}\]

Rewrite each equation:

(58)#\[\begin{align} \begin{cases} m\,\ddot{x}_1 + 2k\,x_1 - k\,x_2 = 0,\\ m\,\ddot{x}_2 - k\,x_1 + 2k\,x_2 = 0. \end{cases} \end{align}\]

We can write \(\mathbf{x} = \begin{pmatrix}x_1 \\ x_2\end{pmatrix}\) and express the system as:

(59)#\[\begin{align} m \,\ddot{\mathbf{x}} + K\,\mathbf{x} = \mathbf{0}, \end{align}\]

where

(60)#\[\begin{align} m \,\ddot{\mathbf{x}} = m \begin{pmatrix}\ddot{x}_1 \\[6pt] \ddot{x}_2\end{pmatrix}, \quad K = \begin{pmatrix} 2k & -k \\ -k & 2k \end{pmatrix}. \end{align}\]

Equivalently,

(61)#\[\begin{align} \ddot{\mathbf{x}} + \frac{1}{m}\,K \,\mathbf{x} = \mathbf{0}. \end{align}\]

This is a second-order linear system describing small oscillations.

We look for solutions of the form

(62)#\[\begin{align} \mathbf{x}(t) = \mathbf{x}(0)\, e^{\,i\,\omega\,t}, \end{align}\]

where \(\mathbf{x}(0)\) is the initial condition and \(\omega\) is the (angular) oscillation frequency.

Plugging into \(m\,\ddot{\mathbf{x}} + K\,\mathbf{x} = 0\) gives:

(63)#\[\begin{align} -\,m\,\omega^2 \,\mathbf{X} + K\,\mathbf{X} = \mathbf{0} \quad \Longrightarrow \quad \left(K - m\,\omega^2 I\right)\,\mathbf{X} = \mathbf{0}. \end{align}\]

Nontrivial solutions exist only if

(64)#\[\begin{align} \det(K - m\,\omega^2 I) = 0, \end{align}\]

which is the eigenvalue problem for \(\omega^2\).

Explicitly, \(K - m\,\omega^2 I\) is:

(65)#\[\begin{align} \begin{pmatrix} 2k - m\,\omega^2 & -k \\ -k & 2k - m\,\omega^2 \end{pmatrix}. \end{align}\]

The determinant is:

(66)#\[\begin{align} (2k - m\,\omega^2)(2k - m\,\omega^2) - (-k)(-k) = (2k - m\,\omega^2)^2 - k^2. \end{align}\]

Setting this to zero results

(67)#\[\begin{align} 2k - m\,\omega^2 = \pm\,k. \end{align}\]

Hence, we get two solutions for \(\omega^2\):

\(\omega_+^2\): taking the \(+\) sign:

(68)#\[\begin{align} 2k - m\,\omega_+^2 = k \quad \Longrightarrow \quad \omega_+^2 = \frac{k}{m} \quad \Longrightarrow \quad \omega_1 = \sqrt{\frac{k}{m}}. \end{align}\]
\(\omega_-^2\): taking the \(-\) sign:

(69)#\[\begin{align} 2k - m\,\omega_-^2 = -\,k \quad \Longrightarrow \quad \omega_-^2 = \frac{3k}{m} \quad \Longrightarrow \quad \omega_2 = \sqrt{\frac{3k}{m}}. \end{align}\]

For each of the normal modes:

Lower Frequency \(\omega_+ = \sqrt{k/m}\): Plug \(\omega_+^2 = k/m\) back into \((K - m\,\omega_+^2 I)\mathbf{X} = 0\). For instance,

(70)#\[\begin{align} \begin{pmatrix} 2k - k & -k \\ -k & 2k - k \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} k & -k \\ -k & k \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \mathbf{0}. \end{align}\]

This implies \(x_1 = x_2\). Physically, the in-phase mode has both masses moving together.

Higher Frequency \(\omega_- = \sqrt{3k/m}\):

(71)#\[\begin{align} \begin{pmatrix} 2k - 3k & -k \\ -k & 2k - 3k \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} -k & -k \\ -k & -k \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \mathbf{0}. \end{align}\]

This yields \(x_1 = -x_2\). Physically, the out-of-phase mode has the two masses moving in opposite directions.

We can compute the position of these coupled oscillators according to the analytical solutions.

# Physical constants
m = 1.0     # mass
k = 1.0     # spring constant

# Frequencies for two normal modes
omegap = np.sqrt(k/m)      # in-phase
omegam = np.sqrt(3*k/m)    # out-of-phase

# Initial conditions
x1_0 = 0
x2_0 = 0.5

# The analytical solution:
def X_analytic(t):
    xp_0 = (x1_0 + x2_0) / 2
    xm_0 = (x1_0 - x2_0) / 2

    xp = xp_0 * np.cos(omegap * t)
    xm = xm_0 * np.cos(omegam * t)

    return np.array([xp + xm, xp - xm])

Plot multiple frames:

from pathlib import Path

from tqdm import tqdm

import matplotlib.pyplot    as plt
import matplotlib.animation as animation

def mkplots(X, t_max=10, n_frames=201):
    T = np.linspace(0, t_max, n_frames)

    Path("plots").mkdir(parents=True, exist_ok=True)
    Xs = []
    for t in T:
        Xs.append(X(t))
    Xs = np.array(Xs)

    for i, t in tqdm(enumerate(T)):
        plt.axhline(y=T[i], color='k', zorder=-1)
        for j in range(Xs.shape[-1]):
            plt.plot(j+1+Xs[:i+1,j], T[:i+1])
            plt.scatter(j+1+Xs[i,j], T[i])
        plt.xlim(0, Xs.shape[-1]+1)        
        plt.xlabel(r'$x_i$')
        plt.ylabel(r'$t$')
        plt.savefig(f"plots/{i:04}.png")
        plt.close()

! rm -rf plots/
mkplots(X_analytic)

0it [00:00, ?it/s]

1it [00:00,  7.67it/s]

3it [00:00, 10.88it/s]

5it [00:00, 11.39it/s]

7it [00:00, 11.83it/s]

9it [00:00, 11.85it/s]

11it [00:00, 12.28it/s]

13it [00:01, 11.26it/s]

15it [00:01, 11.55it/s]

17it [00:01, 11.69it/s]

19it [00:01, 12.10it/s]

21it [00:01, 12.35it/s]

23it [00:01, 12.50it/s]

25it [00:02, 12.42it/s]

27it [00:02, 12.43it/s]

29it [00:02, 12.35it/s]

31it [00:02, 10.99it/s]

33it [00:02, 11.21it/s]

35it [00:02, 11.48it/s]

37it [00:03, 11.63it/s]

39it [00:03, 11.71it/s]

41it [00:03, 11.71it/s]

43it [00:03, 12.14it/s]

45it [00:03, 12.46it/s]

47it [00:03, 12.67it/s]

49it [00:04, 11.03it/s]

51it [00:04, 11.51it/s]

53it [00:04, 11.85it/s]

55it [00:04, 12.12it/s]

57it [00:04, 12.31it/s]

59it [00:04, 12.39it/s]

61it [00:05, 12.42it/s]

63it [00:05, 12.44it/s]

65it [00:05, 12.41it/s]

67it [00:05, 12.41it/s]

69it [00:05, 10.22it/s]

71it [00:06, 10.70it/s]

73it [00:06, 11.08it/s]

75it [00:06, 11.38it/s]

77it [00:06, 11.59it/s]

79it [00:06, 11.63it/s]

81it [00:06, 11.66it/s]

83it [00:07, 11.89it/s]

85it [00:07, 12.24it/s]

87it [00:07, 12.52it/s]

89it [00:07, 12.72it/s]

91it [00:07, 12.88it/s]

93it [00:07, 12.97it/s]

95it [00:08, 10.29it/s]

97it [00:08, 10.97it/s]

99it [00:08, 11.49it/s]

101it [00:08, 11.87it/s]

103it [00:08, 12.18it/s]

105it [00:08, 12.40it/s]

107it [00:09, 12.54it/s]

109it [00:09, 12.63it/s]

111it [00:09, 12.67it/s]

113it [00:09, 12.73it/s]

115it [00:09, 12.78it/s]

117it [00:09, 12.68it/s]

119it [00:09, 12.60it/s]

121it [00:10, 12.47it/s]

123it [00:10, 12.50it/s]

125it [00:10, 12.53it/s]

127it [00:10, 12.52it/s]

129it [00:10,  9.43it/s]

131it [00:11, 10.15it/s]

133it [00:11, 10.75it/s]

135it [00:11, 11.17it/s]

137it [00:11, 11.45it/s]

139it [00:11, 11.64it/s]

141it [00:11, 11.78it/s]

143it [00:12, 11.86it/s]

145it [00:12, 11.92it/s]

147it [00:12, 11.95it/s]

149it [00:12, 11.93it/s]

151it [00:12, 11.94it/s]

153it [00:12, 11.95it/s]

155it [00:13, 11.86it/s]

157it [00:13, 11.77it/s]

159it [00:13, 11.75it/s]

161it [00:13, 11.76it/s]

163it [00:13, 11.74it/s]

165it [00:13, 11.89it/s]

167it [00:14,  8.30it/s]

169it [00:14,  9.27it/s]

171it [00:14, 10.12it/s]

173it [00:14, 10.85it/s]

175it [00:14, 11.38it/s]

177it [00:15, 11.82it/s]

179it [00:15, 12.18it/s]

181it [00:15, 12.15it/s]

183it [00:15, 12.38it/s]

185it [00:15, 12.57it/s]

187it [00:15, 12.72it/s]

189it [00:16, 12.79it/s]

191it [00:16, 12.84it/s]

193it [00:16, 12.78it/s]

195it [00:16, 12.75it/s]

197it [00:16, 12.66it/s]

199it [00:16, 12.64it/s]

201it [00:17, 12.61it/s]

201it [00:17, 11.82it/s]

Can combine them into a movie using ffmpeg:

# This installs `ffmpeg` if it is not available

! if [ ! $(which ffmpeg) ]; then apt update && apt install ffmpeg; fi

Reading package lists... 0%

Reading package lists... 100%

Reading package lists... Done

E: Could not open lock file /var/lib/apt/lists/lock - open (13: Permission denied)
E: Unable to lock directory /var/lib/apt/lists/
W: Problem unlinking the file /var/cache/apt/pkgcache.bin - RemoveCaches (13: Permission denied)
W: Problem unlinking the file /var/cache/apt/srcpkgcache.bin - RemoveCaches (13: Permission denied)

# This convert all image files in "plots/" into "movie.mpg"

! rm -rf movie-2.mpg && ffmpeg -i plots/%04d.png -qmax 2 movie-2.mpg

/usr/bin/sh: 1: ffmpeg: not found

Two Coupled Oscillators–Semi-Analytical/Numerical Solution#

Instead of solving the coupled oscillator problem analytically, we can at least solve the eigenvalue part of the problem numerically.

# HANDSON: Step 1. rewrite the analytical solution in matrix form

# Physical constants
m = 1.0     # mass
k = 1.0     # spring constant

# Frequencies for two normal modes
Omega = np.array([np.sqrt(k/m), np.sqrt(3*k/m)]) # this should become a numpy array

# Initial conditions
X0 = np.array([0, 0.5]) # this should become a numpy array
M0 = np.array([
    [1/2,  1/2],
    [1/2, -1/2],
]) @ X0 # apply an transformation to rewrite the transformation in terms of eigenvectors

# The analytical solution in matrix notation:
def X_matrix(t): # closure on `M0` and `Omega`
    M = M0 * np.cos(Omega * t)
    return np.array([
        [1,  1],
        [1, -1],
    ]) @ M # apply an inverse transformation to rewrite the modes in terms of x1 and x2

print(X_analytic(1))
print(X_matrix(1))

[0.17521471 0.09493644]
[0.17521471 0.09493644]

# HANDSON: Step 2. Replace the manual solutions of eigenvalues Omega and the transform by calling `np.linalg.eig()`

K = np.array([
    [2*k/m, - k/m],
    [- k/m, 2*k/m],
])

# Initial conditions
X0 = np.array([0, 0.5]) # this should become a numpy array

# The semi-analytical solution in matrix notation:
Omega2, V = np.linalg.eig(K)
Omega     = np.sqrt(Omega2)
M0        = V.T @ X0

def X_numeric(t): # closure on `M0` and `Omega`
    return V @ (M0 * np.cos(Omega * t))

print(X_analytic(1))
print(X_numeric(1))

[0.17521471 0.09493644]
[0.17521471 0.09493644]

# HANDSON: Step 3. Generalize the solution to work for arbitrary number of coupled oscillators

K = np.array([
    [2*k/m, - k/m,   0  ],
    [- k/m, 2*k/m, - k/m],
    [  0,   - k/m, 2*k/m],
])

# Initial conditions
X0 = np.array([0,0,0.5]) #should become a numpy array

# The semi-analytical solution in matrix notation:
Omega2, V = np.linalg.eig(K)
Omega     = np.sqrt(Omega2)
M0        = V.T @ X0

! rm -rf plots/
mkplots(X_numeric)
! rm -rf movie-3.mpg && ffmpeg -i plots/%04d.png -qmax 2 movie-3.mpg

0it [00:00, ?it/s]

2it [00:00, 11.31it/s]

4it [00:00, 11.06it/s]

6it [00:00, 10.91it/s]

8it [00:00, 10.78it/s]

10it [00:00, 10.81it/s]

12it [00:01, 10.93it/s]

14it [00:01, 10.93it/s]

16it [00:01, 10.83it/s]

18it [00:02,  4.82it/s]

20it [00:02,  5.87it/s]

22it [00:02,  6.81it/s]

24it [00:02,  7.67it/s]

26it [00:03,  8.38it/s]

28it [00:03,  8.94it/s]

30it [00:03,  9.34it/s]

32it [00:03,  8.47it/s]

33it [00:03,  8.69it/s]

35it [00:04,  9.19it/s]

37it [00:04,  9.51it/s]

39it [00:04,  9.73it/s]

41it [00:04,  9.76it/s]

43it [00:04, 10.18it/s]

45it [00:05, 10.43it/s]

47it [00:05, 10.67it/s]

49it [00:05, 10.72it/s]

51it [00:05,  9.04it/s]

53it [00:05,  9.55it/s]

55it [00:06,  9.91it/s]

57it [00:06, 10.19it/s]

59it [00:06, 10.36it/s]

61it [00:06, 10.50it/s]

63it [00:06, 10.53it/s]

65it [00:07, 10.56it/s]

67it [00:07, 10.55it/s]

69it [00:07, 10.53it/s]

71it [00:07, 10.52it/s]

73it [00:07,  8.14it/s]

74it [00:08,  8.28it/s]

76it [00:08,  8.86it/s]

78it [00:08,  9.25it/s]

79it [00:08,  9.35it/s]

80it [00:08,  9.48it/s]

81it [00:08,  9.48it/s]

82it [00:08,  9.57it/s]

84it [00:09, 10.13it/s]

86it [00:09, 10.50it/s]

88it [00:09, 10.69it/s]

90it [00:09, 10.81it/s]

92it [00:09, 10.88it/s]

94it [00:09, 10.97it/s]

96it [00:10, 10.88it/s]

98it [00:10, 10.79it/s]

100it [00:10,  7.95it/s]

102it [00:10,  8.59it/s]

104it [00:11,  9.14it/s]

106it [00:11,  9.58it/s]

108it [00:11,  9.95it/s]

110it [00:11, 10.25it/s]

112it [00:11, 10.38it/s]

114it [00:12, 10.50it/s]

116it [00:12, 10.55it/s]

118it [00:12, 10.51it/s]

120it [00:12, 10.48it/s]

122it [00:12, 10.44it/s]

124it [00:12, 10.44it/s]

126it [00:13, 10.42it/s]

128it [00:13, 10.46it/s]

130it [00:13, 10.49it/s]

132it [00:13,  7.48it/s]

134it [00:14,  8.21it/s]

136it [00:14,  8.77it/s]

138it [00:14,  9.20it/s]

140it [00:14,  9.49it/s]

142it [00:14,  9.69it/s]

144it [00:15,  9.89it/s]

146it [00:15,  9.96it/s]

148it [00:15, 10.01it/s]

150it [00:15, 10.01it/s]

152it [00:15,  9.99it/s]

154it [00:16, 10.03it/s]

156it [00:16,  9.95it/s]

157it [00:16,  9.91it/s]

158it [00:16,  9.85it/s]

159it [00:16,  9.86it/s]

160it [00:16,  9.82it/s]

161it [00:16,  9.81it/s]

162it [00:16,  9.83it/s]

164it [00:17,  9.92it/s]

166it [00:17, 10.28it/s]

168it [00:17, 10.45it/s]

170it [00:17, 10.51it/s]

172it [00:18,  6.74it/s]

174it [00:18,  7.64it/s]

176it [00:18,  8.40it/s]

178it [00:18,  9.04it/s]

180it [00:18,  9.49it/s]

182it [00:19,  9.81it/s]

184it [00:19, 10.12it/s]

186it [00:19, 10.37it/s]

188it [00:19, 10.52it/s]

190it [00:19, 10.62it/s]

192it [00:20, 10.69it/s]

194it [00:20, 10.72it/s]

196it [00:20, 10.69it/s]

198it [00:20, 10.68it/s]

200it [00:20, 10.61it/s]

201it [00:20,  9.60it/s]

/usr/bin/sh: 1: ffmpeg: not found

N = 4
K = (np.diag(np.repeat(2*k/m, N  )    ) +
     np.diag(np.repeat(- k/m, N-1), +1) +
     np.diag(np.repeat(- k/m, N-1), -1) )

print(K)

# Initial conditions
X0 = np.concatenate([np.zeros(N-1), [0.5]])

# The semi-analytical solution in matrix notation:
Omega2, V = np.linalg.eig(K)
Omega     = np.sqrt(Omega2)
M0        = V.T @ X0

[[ 2. -1.  0.  0.]
 [-1.  2. -1.  0.]
 [ 0. -1.  2. -1.]
 [ 0.  0. -1.  2.]]

! rm -rf plots/
mkplots(X_numeric)
! rm -rf movie-4.mpg && ffmpeg -i plots/%04d.png -qmax 2 movie-4.mpg

0it [00:00, ?it/s]

2it [00:00, 11.12it/s]

4it [00:00, 10.95it/s]

6it [00:00, 10.82it/s]

8it [00:00, 10.78it/s]

10it [00:00, 10.84it/s]

12it [00:01, 10.90it/s]

14it [00:01, 10.79it/s]

16it [00:01, 10.61it/s]

18it [00:01, 10.64it/s]

20it [00:01, 10.91it/s]

22it [00:02, 10.95it/s]

24it [00:03,  4.39it/s]

26it [00:03,  5.36it/s]

28it [00:03,  6.30it/s]

30it [00:03,  7.17it/s]

32it [00:03,  7.91it/s]

34it [00:04,  8.55it/s]

36it [00:04,  9.00it/s]

38it [00:04,  9.33it/s]

40it [00:04,  8.23it/s]

42it [00:04,  8.82it/s]

44it [00:05,  9.47it/s]

46it [00:05,  9.98it/s]

48it [00:05, 10.36it/s]

50it [00:05, 10.59it/s]

52it [00:05, 10.71it/s]

54it [00:06, 10.74it/s]

56it [00:06, 10.76it/s]

58it [00:06, 10.80it/s]

60it [00:06, 10.78it/s]

62it [00:06,  8.61it/s]

64it [00:07,  9.10it/s]

66it [00:07,  9.47it/s]

68it [00:07,  9.72it/s]

70it [00:07,  9.91it/s]

72it [00:07, 10.04it/s]

74it [00:08, 10.14it/s]

76it [00:08, 10.25it/s]

78it [00:08, 10.27it/s]

80it [00:08, 10.13it/s]

82it [00:08, 10.17it/s]

84it [00:09, 10.50it/s]

86it [00:09,  8.42it/s]

88it [00:09,  9.10it/s]

90it [00:09,  9.70it/s]

92it [00:09, 10.14it/s]

94it [00:10, 10.50it/s]

96it [00:10, 10.75it/s]

98it [00:10, 10.89it/s]

100it [00:10, 10.97it/s]

102it [00:10, 10.84it/s]

104it [00:10, 10.95it/s]

106it [00:11, 10.98it/s]

108it [00:11, 11.03it/s]

110it [00:11, 11.11it/s]

112it [00:11, 10.41it/s]

114it [00:11, 10.42it/s]

116it [00:12, 10.60it/s]

118it [00:12,  7.82it/s]

120it [00:12,  8.52it/s]

121it [00:12,  8.75it/s]

123it [00:12,  9.30it/s]

125it [00:13,  9.72it/s]

127it [00:13, 10.08it/s]

129it [00:13, 10.25it/s]

131it [00:13, 10.39it/s]

133it [00:13, 10.49it/s]

135it [00:14, 10.52it/s]

137it [00:14, 10.54it/s]

139it [00:14, 10.47it/s]

141it [00:14, 10.52it/s]

143it [00:14, 10.50it/s]

145it [00:15, 10.50it/s]

147it [00:15, 10.53it/s]

149it [00:15, 10.52it/s]

151it [00:15, 10.53it/s]

153it [00:15, 10.41it/s]

155it [00:16,  7.16it/s]

157it [00:16,  7.86it/s]

159it [00:16,  8.47it/s]

160it [00:16,  8.69it/s]

161it [00:16,  8.90it/s]

163it [00:17,  9.36it/s]

164it [00:17,  9.45it/s]

166it [00:17, 10.03it/s]

168it [00:17, 10.48it/s]

170it [00:17, 10.77it/s]

172it [00:17, 10.87it/s]

174it [00:18, 10.95it/s]

176it [00:18, 10.96it/s]

178it [00:18, 11.03it/s]

180it [00:18, 11.07it/s]

182it [00:18, 11.12it/s]

184it [00:18, 11.12it/s]

186it [00:19, 11.14it/s]

188it [00:19, 11.20it/s]

190it [00:19, 11.18it/s]

192it [00:19, 11.20it/s]

194it [00:19, 11.03it/s]

196it [00:20, 11.03it/s]

198it [00:20, 11.01it/s]

200it [00:20, 11.02it/s]

201it [00:20,  9.79it/s]

/usr/bin/sh: 1: ffmpeg: not found

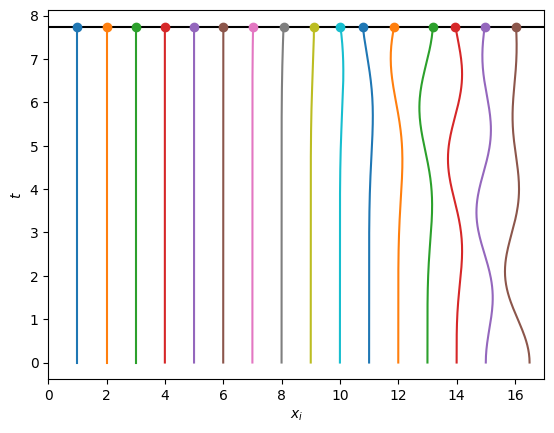
N = 16
K = (np.diag(np.repeat(2*k/m, N  )    ) +
     np.diag(np.repeat(- k/m, N-1), +1) +
     np.diag(np.repeat(- k/m, N-1), -1) )

print(K)

# Initial conditions
X0 = np.concatenate([np.zeros(N-1), [0.5]])

# The semi-analytical solution in matrix notation:
Omega2, V = np.linalg.eig(K)
Omega     = np.sqrt(Omega2)
M0        = V.T @ X0

[[ 2. -1.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [-1.  2. -1.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0. -1.  2. -1.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0. -1.  2. -1.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0. -1.  2. -1.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0. -1.  2. -1.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0. -1.  2. -1.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0. -1.  2. -1.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0. -1.  2. -1.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0. -1.  2. -1.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0. -1.  2. -1.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  0. -1.  2. -1.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0. -1.  2. -1.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0. -1.  2. -1.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0. -1.  2. -1.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0. -1.  2.]]

! rm -rf plots/
mkplots(X_numeric, t_max=100, n_frames=2001)
! rm -rf movie-16.mpg && ffmpeg -i plots/%04d.png -qmax 2 movie-16.mpg

0it [00:00, ?it/s]

1it [00:00,  5.69it/s]

2it [00:01,  1.51it/s]

3it [00:01,  2.28it/s]

4it [00:01,  2.99it/s]

5it [00:01,  3.58it/s]

6it [00:01,  4.08it/s]

7it [00:02,  4.49it/s]

8it [00:02,  4.79it/s]

9it [00:02,  5.02it/s]

10it [00:02,  5.27it/s]

11it [00:02,  5.39it/s]

12it [00:02,  5.51it/s]

13it [00:03,  4.96it/s]

14it [00:03,  5.15it/s]

15it [00:03,  5.31it/s]

16it [00:03,  5.40it/s]

17it [00:03,  5.43it/s]

18it [00:04,  5.53it/s]

19it [00:04,  5.60it/s]

20it [00:04,  5.66it/s]

21it [00:04,  5.70it/s]

22it [00:04,  5.71it/s]

23it [00:04,  5.72it/s]

24it [00:05,  4.94it/s]

25it [00:05,  5.17it/s]

26it [00:05,  5.32it/s]

27it [00:05,  5.43it/s]

28it [00:05,  5.48it/s]

29it [00:06,  5.52it/s]

30it [00:06,  5.44it/s]

31it [00:06,  5.50it/s]

32it [00:06,  5.52it/s]

33it [00:06,  5.52it/s]

34it [00:06,  5.55it/s]

35it [00:07,  4.64it/s]

36it [00:07,  4.92it/s]

37it [00:07,  5.11it/s]

38it [00:07,  5.25it/s]

39it [00:07,  5.33it/s]

40it [00:08,  5.39it/s]

41it [00:08,  5.44it/s]

42it [00:08,  5.59it/s]

43it [00:08,  5.70it/s]

44it [00:08,  5.77it/s]

45it [00:09,  5.80it/s]

46it [00:09,  5.76it/s]

47it [00:09,  5.79it/s]

48it [00:09,  5.81it/s]

49it [00:09,  5.80it/s]

50it [00:10,  4.40it/s]

51it [00:10,  4.72it/s]

52it [00:10,  4.98it/s]

53it [00:10,  5.19it/s]

54it [00:10,  5.35it/s]

55it [00:10,  5.46it/s]

56it [00:11,  5.55it/s]

57it [00:11,  5.60it/s]

58it [00:11,  5.61it/s]

59it [00:11,  5.64it/s]

60it [00:11,  5.65it/s]

61it [00:12,  5.67it/s]

62it [00:12,  5.69it/s]

63it [00:12,  5.69it/s]

64it [00:12,  5.70it/s]

65it [00:12,  5.70it/s]

66it [00:12,  5.71it/s]

67it [00:13,  5.74it/s]

68it [00:13,  4.22it/s]

69it [00:13,  4.57it/s]

70it [00:13,  4.83it/s]

71it [00:13,  5.06it/s]

72it [00:14,  5.22it/s]

73it [00:14,  5.32it/s]

74it [00:14,  5.39it/s]

75it [00:14,  5.42it/s]

76it [00:14,  5.46it/s]

77it [00:15,  5.49it/s]

78it [00:15,  5.49it/s]

79it [00:15,  5.52it/s]

80it [00:15,  5.54it/s]

81it [00:15,  5.53it/s]

82it [00:15,  5.55it/s]

83it [00:16,  5.65it/s]

84it [00:16,  5.72it/s]

85it [00:16,  5.78it/s]

86it [00:16,  5.80it/s]

87it [00:16,  5.84it/s]

88it [00:16,  5.86it/s]

89it [00:17,  5.85it/s]

90it [00:17,  5.87it/s]

91it [00:17,  3.99it/s]

92it [00:17,  4.39it/s]

93it [00:18,  4.76it/s]

94it [00:18,  5.05it/s]

95it [00:18,  5.30it/s]

96it [00:18,  5.48it/s]

97it [00:18,  5.57it/s]

98it [00:18,  5.61it/s]

99it [00:19,  5.65it/s]

100it [00:19,  5.66it/s]

101it [00:19,  5.70it/s]

102it [00:19,  5.70it/s]

103it [00:19,  5.72it/s]

104it [00:19,  5.73it/s]

105it [00:20,  5.73it/s]

106it [00:20,  5.74it/s]

107it [00:20,  5.76it/s]

108it [00:20,  5.77it/s]

109it [00:20,  5.79it/s]

110it [00:21,  5.80it/s]

111it [00:21,  5.77it/s]

112it [00:21,  5.76it/s]

113it [00:21,  5.74it/s]

114it [00:21,  5.77it/s]

115it [00:21,  5.75it/s]

116it [00:22,  5.75it/s]

117it [00:22,  5.74it/s]

118it [00:22,  5.72it/s]

119it [00:22,  3.53it/s]

120it [00:23,  4.00it/s]

121it [00:23,  4.37it/s]

122it [00:23,  4.71it/s]

123it [00:23,  4.99it/s]

124it [00:23,  5.16it/s]

125it [00:24,  5.32it/s]

126it [00:24,  5.45it/s]

127it [00:24,  5.52it/s]

128it [00:24,  5.59it/s]

129it [00:24,  5.63it/s]

130it [00:24,  5.65it/s]

131it [00:25,  5.69it/s]

132it [00:25,  5.68it/s]

133it [00:25,  5.69it/s]

134it [00:25,  5.72it/s]

135it [00:25,  5.71it/s]

136it [00:25,  5.70it/s]

137it [00:26,  5.71it/s]

138it [00:26,  5.70it/s]

139it [00:26,  5.66it/s]

140it [00:26,  5.67it/s]

141it [00:26,  5.67it/s]

142it [00:26,  5.69it/s]

143it [00:27,  5.68it/s]

144it [00:27,  5.68it/s]

145it [00:27,  5.69it/s]

146it [00:27,  5.70it/s]

147it [00:27,  5.70it/s]

148it [00:28,  5.72it/s]

149it [00:28,  5.72it/s]

150it [00:28,  5.69it/s]

151it [00:28,  5.71it/s]

152it [00:28,  5.70it/s]

153it [00:29,  3.26it/s]

154it [00:29,  3.73it/s]

155it [00:29,  4.16it/s]

155it [00:29,  5.19it/s]

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[19], line 2
      1 get_ipython().system(' rm -rf plots/')
----> 2 mkplots(X_numeric, t_max=100, n_frames=2001)
      3 get_ipython().system(' rm -rf movie-16.mpg && ffmpeg -i plots/%04d.png -qmax 2 movie-16.mpg')

Cell In[6], line 25, in mkplots(X, t_max, n_frames)
     23 plt.xlabel(r'$x_i$')
     24 plt.ylabel(r'$t$')
---> 25 plt.savefig(f"plots/{i:04}.png")
     26 plt.close()

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/pyplot.py:1244, in savefig(*args, **kwargs)
   1241 # savefig default implementation has no return, so mypy is unhappy
   1242 # presumably this is here because subclasses can return?
   1243 res = fig.savefig(*args, **kwargs)  # type: ignore[func-returns-value]
-> 1244 fig.canvas.draw_idle()  # Need this if 'transparent=True', to reset colors.
   1245 return res

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/backend_bases.py:1891, in FigureCanvasBase.draw_idle(self, *args, **kwargs)
   1889 if not self._is_idle_drawing:
   1890     with self._idle_draw_cntx():
-> 1891         self.draw(*args, **kwargs)

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/backends/backend_agg.py:382, in FigureCanvasAgg.draw(self)
    379 # Acquire a lock on the shared font cache.
    380 with (self.toolbar._wait_cursor_for_draw_cm() if self.toolbar
    381       else nullcontext()):
--> 382     self.figure.draw(self.renderer)
    383     # A GUI class may be need to update a window using this draw, so
    384     # don't forget to call the superclass.
    385     super().draw()

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/artist.py:94, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     92 @wraps(draw)
     93 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 94     result = draw(artist, renderer, *args, **kwargs)
     95     if renderer._rasterizing:
     96         renderer.stop_rasterizing()

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/figure.py:3257, in Figure.draw(self, renderer)
   3254             # ValueError can occur when resizing a window.
   3256     self.patch.draw(renderer)
-> 3257     mimage._draw_list_compositing_images(
   3258         renderer, self, artists, self.suppressComposite)
   3260     renderer.close_group('figure')
   3261 finally:

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/axes/_base.py:3210, in _AxesBase.draw(self, renderer)
   3207 if artists_rasterized:
   3208     _draw_rasterized(self.get_figure(root=True), artists_rasterized, renderer)
-> 3210 mimage._draw_list_compositing_images(
   3211     renderer, self, artists, self.get_figure(root=True).suppressComposite)
   3213 renderer.close_group('axes')
   3214 self.stale = False

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/image.py:134, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    132 if not_composite or not has_images:
    133     for a in artists:
--> 134         a.draw(renderer)
    135 else:
    136     # Composite any adjacent images together
    137     image_group = []

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/axis.py:1408, in Axis.draw(self, renderer)
   1405 tlb1, tlb2 = self._get_ticklabel_bboxes(ticks_to_draw, renderer)
   1407 for tick in ticks_to_draw:
-> 1408     tick.draw(renderer)
   1410 # Shift label away from axes to avoid overlapping ticklabels.
   1411 self._update_label_position(renderer)

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/axis.py:276, in Tick.draw(self, renderer)
    273 renderer.open_group(self.__name__, gid=self.get_gid())
    274 for artist in [self.gridline, self.tick1line, self.tick2line,
    275                self.label1, self.label2]:
--> 276     artist.draw(renderer)
    277 renderer.close_group(self.__name__)
    278 self.stale = False

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/artist.py:71, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     68     if artist.get_agg_filter() is not None:
     69         renderer.start_filter()
---> 71     return draw(artist, renderer)
     72 finally:
     73     if artist.get_agg_filter() is not None:

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/text.py:752, in Text.draw(self, renderer)
    749 renderer.open_group('text', self.get_gid())
    751 with self._cm_set(text=self._get_wrapped_text()):
--> 752     bbox, info, descent = self._get_layout(renderer)
    753     trans = self.get_transform()
    755     # don't use self.get_position here, which refers to text
    756     # position in Text:

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/text.py:506, in Text._get_layout(self, renderer)
    503 bbox = Bbox.from_bounds(xmin, ymin, width, height)
    505 # now rotate the positions around the first (x, y) position
--> 506 xys = M.transform(offset_layout) - (offsetx, offsety)
    508 return bbox, list(zip(lines, zip(ws, hs), *xys.T)), descent

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/transforms.py:1784, in AffineBase.transform(self, values)
   1782 def transform(self, values):
   1783     # docstring inherited
-> 1784     return self.transform_affine(values)

File /opt/hostedtoolcache/Python/3.12.10/x64/lib/python3.12/site-packages/matplotlib/transforms.py:1853, in Affine2DBase.transform_affine(self, values)
   1851     tpoints = affine_transform(values.data, mtx)
   1852     return np.ma.MaskedArray(tpoints, mask=np.ma.getmask(values))
-> 1853 return affine_transform(values, mtx)

KeyboardInterrupt: 

../_images/217faf17dbedd1d4184177836c0c7d8bfcc6c0925950def193c48a153041e375.png